AILab Howest

Voorbeelden van veelvoorkomende optimalisatieproblemen

Enkele klassiekers uit de wereld van de combinatorische optimalisatie:

• Knapsack-probleem: hoe kies je een subset van objecten met een bepaalde waarde en gewicht, zodat je zo veel mogelijk waarde in één rugzak stopt zonder het gewichtslimiet te overschrijden?
• Bin packing: hoe verdeel je objecten over zo weinig mogelijk bakken zonder de maximale capaciteit van een bak te overschrijden?
• Traveling Salesman Problem (TSP): wat is de kortste route langs een reeks steden waarbij elke stad exact één keer bezocht wordt?
• Taakplanning: hoe wijs je taken toe aan tijdslots en middelen, rekening houdend met afhankelijkheden en beperkingen?

Een voorbeeld animatie voor het Traveling Salesman Problem

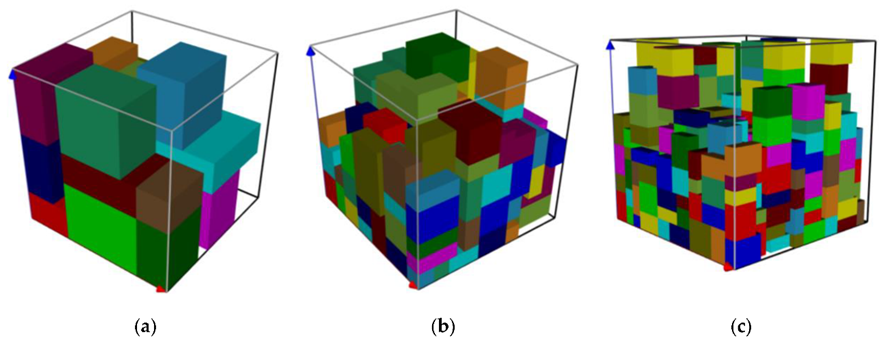
Bin packing problem met 3 bins

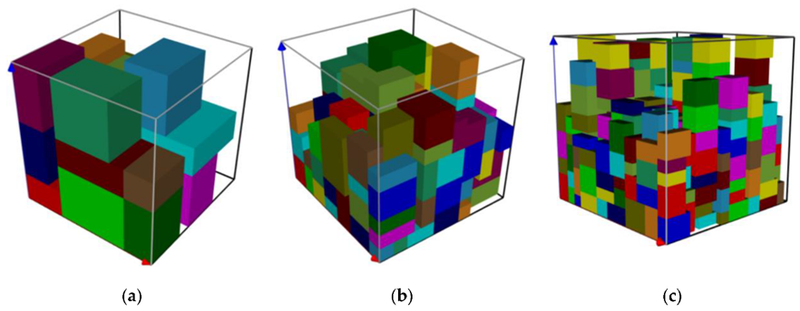
Deze optimalisatieproblemen lijken misschien abstract, maar ze liggen aan de basis van heel wat praktische toepassingen. Het knapsack-probleem kan je bijvoorbeeld toepassen op het optimaliseren van de lading in een vrachtwagen of drone: hoe neem je zo veel mogelijk waardevolle goederen mee zonder het gewichtslimiet te overschrijden? Ook in marketing is dit relevant, bijvoorbeeld bij het selecteren van de meest rendabele combinatie van advertenties binnen een vast budget. Of bij het opstellen van een planning voor een operatiezaal, waarbij je rekening moet houden met verschillende operaties die elk hun eigen duur, beschikbaar personeel en variërende prioriteit hebben.

Veel van deze problemen zijn NP-hard. Dat betekent dat de rekencomplexiteit exponentieel toeneemt met de grootte van het probleem, waardoor brute force geen optie is. In plaats daarvan zoeken we naar slimme heuristieken die goede oplossingen vinden in aanvaardbare tijd. Eén zo'n techniek is het genetisch algoritme.

Genetische algoritmes: evolutie als optimalisatiestrategie

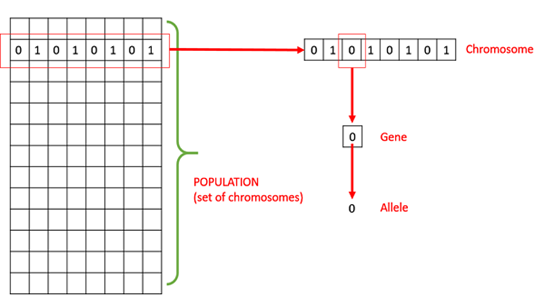
Genetische algoritmes (GAs) zijn geïnspireerd op het proces van natuurlijke selectie. In plaats van één oplossing te verbeteren, werk je met een populatie van oplossingen die over meerdere generaties heen evolueert.

Elke oplossing wordt voorgesteld als een chromosoom: een reeks “genen” die samen de keuzes binnen het probleem coderen. Denk bijvoorbeeld aan een lijst die voor elk object in een bin packing probleem aangeeft in welke doos het zit. Elke combinatie is een mogelijke oplossing.

Het proces verloopt in stappen:

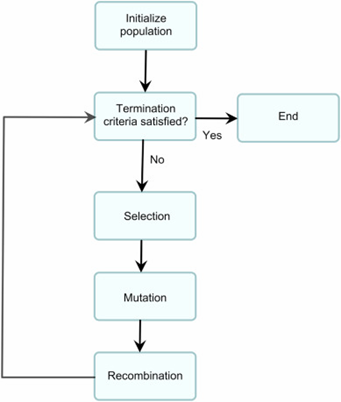
1. Initialisatie
   Een startpopulatie wordt willekeurig gegenereerd. Deze groep bevat een aantal verschillende oplossingskandidaten.
2. Fitnessfunctie
   Elke oplossing wordt geëvalueerd aan de hand van een fitness score. In een bin packing context kan dat bijvoorbeeld gebaseerd zijn op het aantal gebruikte dozen, hoe goed de ruimte is benut, en of er beperkingen geschonden zijn. Hoe hoger de fitness, hoe beter de oplossing.
3. Selectie
   Vervolgens selecteren we de meest veelbelovende oplossingen — de 'fitste' — als ouders voor de volgende generatie. Dit kan via technieken zoals tournament selection, waarbij meerdere oplossingen tegen elkaar “strijden” en de beste wint. Belangrijk is dat voor een optimaal eindresultaat, ook wat minder fitte oplossingen worden meegenomen.
4. Variatie: mutatie en recombinatie
   Door mutatie maken we kleine willekeurige veranderingen (bv. twee items wisselen van plaats). Dit helpt om het zoekgebied te verkennen en lokale optima te vermijden.
   Via recombinatie (of crossover) combineren we eigenschappen van twee of meer ouders om een nieuw kind te vormen. Bijvoorbeeld: bij uniform crossover wordt voor elk gen afzonderlijk beslist of het van ouder 1 of ouder 2 komt.
5. Vervanging
   De nieuwe generatie oplossingen vervangt (gedeeltelijk) de oude. Dat kan op basis van leeftijd (de oudste gaan eruit), of op basis van fitness (de minst succesvolle verdwijnen).
6. Stopcriterium
   Het proces stopt wanneer de verbetering stilvalt, een vooraf bepaald aantal generaties bereikt is, of de fitnessscore een gewenst niveau heeft.

Een van de sterke punten van genetische algoritmes is hun flexibiliteit. Ze kunnen omgaan met complexe, niet-lineaire problemen met veel beperkingen. Bovendien zijn ze relatief eenvoudig te implementeren en kunnen ze makkelijk aangepast worden aan de noden van een specifiek probleem.

Google OR-Tools: krachtige optimalisatiesoftware

Wie liever met een gebruiksklare tool werkt, kan terecht bij Google OR-Tools. Dit is een open-source softwarepakket ontwikkeld door Google, specifiek gericht op het oplossen van combinatorische optimalisatieproblemen.

OR-Tools ondersteunt onder andere:

• Bin packing & knapsack
• Routingsproblemen (zoals TSP)
• Planning & scheduling
• Grafen en netwerken

Hoewel OR-Tools niet per se gebaseerd is op genetische algoritmes, bevat het verschillende krachtige oplossers zoals constraint programming en lokale zoekmethodes. Dankzij de overzichtelijke API’s in Python, Java en C++ is het een praktische keuze voor developers die snel aan de slag willen met real-life optimalisatieproblemen.